• 二分思想
  • 如下图所示：
• 递归思想
• 时间复杂度分析
• 倍增思想
  • 类似的倍增的思想:
• 有哪些痛点
• 标准化
  • left + 1 < right
  • left < right
  • left <= right
• 额外技巧

二分思想

Binary Search是在排序”数组”中查找指定(Any/First/Last/Closest/Range)元素的一种快速搜索算法。

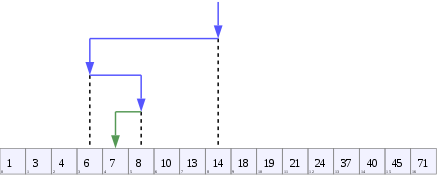
如下图所示：

查找数字7

1. 将数组一分为二，中间的元素14与7比较，由于7 < 14, 目标在左边的一半
2. 将剩余部分一分为二，中间元素6与7比较，由于6 < 7, 目标在右边的一半
3. 沿着图中箭头，不断的把问题缩小一半，直到找到目标

递归思想

二分算法也是递归思想的一种，但这并不意味着二分一定要用递归来实现。

递归过程：

1. 二分搜索，将原问题分为左右两个子问题，中间值与目标对比，抛弃一半不可能的，将问题规模缩小一半
2. 重复步骤1，直到找到目标(或者未找到目标)

时间复杂度分析

二分查找相当于通过O(1)的执行时间(大小比较操作)，把问题缩小一半

# T(N)表示一个问题，所需要的执行时间

T(N) = T(N/2) + O(1)
     = (T(N/4) + O(1)) + O(1)
     = ((T(N/8) + O(1)) + O(1)) + O(1)
     ...
     = T(1) + logN * O(1)
     = O(logN)

那通过O(N)的执行时间，把问题缩小一半呢？

倍增思想

一个无穷大的排序数组Arr，要求寻找目标T，但是内存只能读一部分，该怎么解决呢？要求时间复杂度O(LogT)

1. 如下,首先分别检测第2^K(K>=0)个, 直到找第2^(k-1)个 <= T <= 第2^k个
2. 然后有了上下边界，就可以正常二分了

 第1个    第2个   第4个 
Arr[0], Arr[1], Arr[3], ... Arr[2^(K-1) - 1], Arr[2^K -1]... 

类似的倍增的思想:

1. 指数退避(Exponential backoff): 爬虫访问
2. 数组动态扩容策略: vector(C++), ArrayList(Java)

有哪些痛点

1. 代码死循环，边界条件如何判断
2. 数据溢出，index有溢出的可能
3. 丢掉错误的一半，从而错过正确答案
4. 看不出来，能用二分思想解决

标准化

标准化主要解决1-2条痛点，3-4只能多练习来解决

注意，start=0, end=1. mid=(start + end) // 2, 这里mid=0，也就是说，这个表达式的结果是偏左的

python中引入了新的运算符//, 而原来的/的会保留小数点

正整数情况下和其他语言一样截断，但是负数就会有差异:

mid = (start + end) // 2 = floor((start + rihgt) / 2) # (-7 + -6) // 2 = -7, 结果依然偏左 

mid = (start + end) / 2; // (-7 + -6) / 2 = -6, 结果偏右，如果模版不一致，这个可能会导致死循环

无论是python还是cpp建议使用以下两种方式, 它们可以有效处理正数负数，结果都偏左

mid = (start + end) >> 1
mid = start + (end - start) / 2 # 可以防止溢出

left + 1 < right

不用考虑mid是+1还是-1，只是结果需要额外判断边界

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int start = 0;
        int end = nums.size() - 1;

        while (start + 1 < end) {
            int mid = start + (end - start) / 2;
            if (nums[mid] == target) {
                return mid;
            }

            if (nums[mid] < target) {
                start = mid;
            } else {
                end = mid;
            }
        }

        if (nums[start] == target ) { // 额外判断
            return start;
        } else if (nums[end] == target) {
            return end;
        } else {
            return -1;
        }
    }
};

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int start = -1;
        int end = nums.size(); // 左开右开 (start, end)

        while (start + 1 < end) {
            int mid = start + (end - start) / 2;
            if (nums[mid] == target) {
                return mid;
            }

            if (nums[mid] < target) {
                start = mid;
            } else {
                end = mid;
            }
        }

        return -1;
    }
};

left < right

终止条件left==right, 因为中值偏左, 所以mid = left + 1, 比较简洁, 个人喜欢这个

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int start = 0;
        int end = nums.size() - 1;

        while (start < end) {
            int mid = start + (end - start) / 2;
            if (nums[mid] == target) {
                return mid;
            }

            if (nums[mid] < target) {
                start = mid + 1;
            } else {
                end = mid;
            }
        }

        if (nums[start] == target) { // 额外判断
            return start;
        } else {
            return -1;
        }
    }
};

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int start = 0;
        int end = nums.size();  // 左闭右开 [start, end)

        while (start < end) {
            int mid = start + (end - start) / 2;
            if (nums[mid] == target) {
                return mid;
            }

            if (nums[mid] < target) {
                start = mid + 1;
            } else {
                end = mid;
            }
        }

        return -1;
    }
};

left <= right

终止条件是left > right, 结合上一条, right = mid - 1也要让一步, 比较简洁

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int start = 0;
        int end = nums.size() - 1;  // 闭区间[start, end]

        while (start <= end) {
            int mid = start + (end - start) / 2;
            if (nums[mid] == target) {
                return mid;
            }

            if (nums[mid] < target) {
                start = mid + 1;
            } else {
                end = mid - 1;
            }
        }

        return -1;
    }
};

额外技巧

1. 拿到一道算法题，除了认真审题，理解要求，要尽快确认属于哪类算法
2. 优化一个暴力破解为O(N)的算法，那基本上就只能和二分相关了
3. 问题答案的个数，是该问题算法复杂度的下限
4. 如果数组中，每个元素都发生了改变，那至少需要O(N)的时间复杂度
5. 如何恢复[4,5,6,1,2,3]到[1,2,3,4,5,6]三步翻转法, 中间两步:[6,5,4,1,2,3]=>[6,5,4,3,2,1]

-End-