极客算法

数据结构 - 二叉树BinaryTree

2020-05-14
Algorithm

二叉树

问题1，如果一颗二叉树🌲，有N个节点，那么它的高度用Big O表示是多少呢？

答案是O(N)，因为链表也是一颗独特的二叉树

1 -> 2 -> 3 -> 4 -> 5

二叉树的三种遍历

对于二叉树遍历，它的深度优先搜索DFS，有三种遍历策略，是以遍历root的三种策略命名的

N = Node(节点)

L = Left(左节点)

R = Right(右节点)

在深度优先搜索的时候，以Node的访问顺序，定义了三种不同的搜索策略：

前序遍历：结点 —> 左子树 —> 右子树

中序遍历：左子树—> 结点 —> 右子树

后序遍历：左子树 —> 右子树 —> 结点

前序遍历

前序遍历

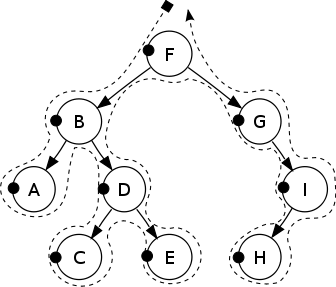
Pre-order: F, B, A, D, C, E, G, I, H.

中序遍历

中序遍历

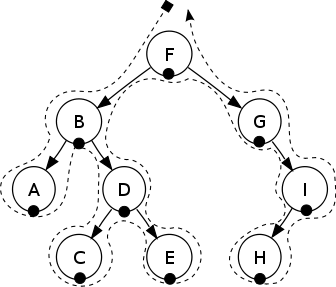
In-order: A, B, C, D, E, F, G, H, I.

在二叉搜索树(BST)中，中序遍历返回递增的一个序列

后序遍历

后序遍历

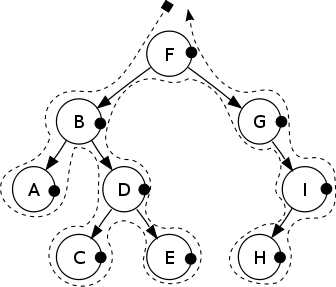
Post-order: A, C, E, D, B, H, I, G, F.

代码实现

递归代码

递归实现比较直观容易，通常DFS遍历，都需要传递一个参数 or 设置一个全局变量，来保存结果

def pre_order(self, node, results):
    if node is None:
        return
    results.append(node.val)
    self.pre_order(node.left, results)
    self.pre_order(node.right, results)

def in_order(self, node, results):
    if node is None:
        return
    self.in_order(node.left, results)
    results.append(node.val)
    self.in_order(node.right, results)

def post_order(self, node, results):
    if node is None:
        return
    self.post_order(node.left, results)
    self.post_order(node.right, results)
    results.append(node.val)

非递归代码

深度优先遍历的非递归代码，一定用到的是stack数据接口

非递归实现前序和中序还可以，后续遍历就非常烧脑了

前序最简单，相当于for循环所有children，所以一版非递归DFS，就用前序就好了。

中序遍历，由于对于BST有一个递增的特性，所以还是比较常用的

def preorderTraversal(self, root):
    results = []
    if root is None:
        return results
    stack = [root]
    while(len(stack) > 0):
        node = stack.pop()
        results.append(node.val)
        # right first so left pop fisrt
        if node.right is not None:
            stack.append(node.right)
        if node.left is not None:
            stack.append(node.left)
    return results

def inorderTraversal(self, root):
    results = []
    if root is None:
        return results
    stack = []
    node = root
    while(len(stack) > 0 or node is not None):
        if (node is not None):
            stack.append(node)
            node = node.left
        else:
            node = stack.pop()
            results.append(node.val)
            node = node.right
    return results

def postorderTraversal(self, root):
    results = []
    if root is None:
        return results
    node = root
    stack = []
    lastNodeVisted = None
    while(len(stack) > 0 or node is not None):
        if node is not None:
            stack.append(node)
            node = node.left
        else:
            peek = stack[-1] # last element
            if (peek.right is not None and lastNodeVisted != peek.right):
                node = peek.right
            else:
                results.append(peek.val)
                lastNodeVisted = stack.pop()
    return results

递归思想

能否使用递归实现，有一个非常重要的判断标准，就是递归的深度。

现代Linux操作系统，stack大小也只有8M，可以通过ulimit -a查看

不论内存有多大，对于程序来说，有个很小的递归上线，深度大概10K左右。

python更小，只有1K层，左右。有兴趣可以文末链接

递归的三要素

  1. 递归的定义
  2. 递归的拆解
  3. 递归的出口

递归的技巧

对于不能返回多个值的语言，可以定一个类，封装多个值返回

时间复杂度分析

通过O(N)的时间，把N的问题变成N/2的问题, 典型的是归并排序

  T(N) = O(N) + 2 * T(N/2)

       = O(N) + 2 * (O(N/2) + 2 * T(N/4)) = O(N) + O(N) + 4 * T(N / 4) 

       = O(N) + O(N) + 4 * (O(N/4) + 2 * T(N/8)) = O(N) + O(N) + O(N) + 8 * T(N/8)

       ...

       = O(N) + O(N) + O(N) ... + N * (N/ N) = O(N) + O(N) + O(N) + ... + N * O(1)

       = O(N * logN) + O(N)

       = O(N * logN)

通过O(1)的时间，把N的问题变成N/2的问题, 典型是二叉树上的分治算法

  T(N) = O(1) + 2 * T(N/2)

       = O(1) + 2 * (O(1) + 2 * T(N/4)) = O(1) + 2 * O(1) + 4 * T(N / 4) 

       = O(1) + 2 * (N) + 4 * (O(1) + 2 * T(N/8)) = O(1) + 2 * O(1) + 4 * O(1) + 8 * T(N/8)

       ...

       = O(1) + 2 * O(1) + 4 * O(1) ... + N * (N/ N) = (2 ^ 0 + 2 ^ 1 + 2 ^ 2 + ... + 2 ^ (logN - 1)) * O(1) + N * O(1)

       = (1 + 2 + 4 + ... + N) * O(1) + N * O(1)

       = (2N - 1) * O(1) + N * O(1) = O(3N - 1)

       = O(N)

递归的两种方式

问题：给出一棵二叉树，返回其节点值的前序遍历

分治算法

特点：

  1. 结果 = 当前值 + 左子树返回值 + 右子树返回值
  2. Bottom-up
def preorderTraversal(self, root):
    return self.traverse(root)
    
def traverse(self, root): # 递归的定义
    if root is None:
        return [] # 递归的出口
      
    results = [] 

    # 递归的拆解-Start
    lefts = self.traverse(root.left)
    rights = self.traverse(root.right)
    
    results.append(root.val)
    results.extend(lefts)
    results.extend(rights)
    
    return results
    # 递归的拆解-End

遍历算法

特点：

  1. 结果 = 一个全局变量results，从根一层层搜集结果
  2. Top-down
def preorderTraversal(self, root):
    results = []
    self.traverse(root, results)
    return results
    
def traverse(self, root, results): # 递归的定义
    if root is None:
        return # 递归的出口

    # 递归的拆解-Start
    results.append(root.val)
    self.traverse(root.left, results)
    self.traverse(root.right, results)
    # 递归的拆解-End

二叉搜索树BST

问题2， 如果一颗二叉搜索树🌲(BST), 有N个节点，那么它的高度用Big O表示是多少呢？

没有提到平衡，BST的高度也有可能是O(N), 例如下图高度=N/2

常用的平衡二叉树有红黑树

      4
    3   5
  2       6
1           7

二叉搜索树BST特点

  1. 左子树都小于root的值(不推荐把等于放在这里)
  2. 右子树都大于root的值(也可以等于)

BST必要不充分特点

对于BST，进行中序遍历，结果是一个不下降序列

参考：

《程序语言递归深度》 https://rosettacode.org/wiki/Find_limit_of_recursion

–End–

上一篇 算法 - 摩尔投票Moore’s Voting

下一篇 算法 - 广度优先搜索BFS

评论

内容:
其他: