BFS & DFS
BFS和DFS是AI中常用的搜索算法
GBFS
BFS和DFS,只是遵守自己的搜素逻辑,没有对特定问题的优化。
假设知道起始点+终止点,人能够从地图上直观的感受,哪一条岔路会离目标更近一些。优先访问”更优”的路径
Greedy Best-first Search(贪心 + BFS)采用了这种更加智慧的方式,这种直观的更接近目标被定义为函数f(n), 可以是平面两点的距离,也可以是其他启发式的方式。
PS: 启发式=Heurestic(involving or serving as an aid to learning, discovery, or problem-solving by experimental(经验) and especially trial-and-erro(试错) methods)
启发式函数
曼哈顿距离
想象在一个棋盘或城市街道网格上,只能沿着水平或垂直的方向移动,不能斜着走, 适用于在网格状图(如迷宫)中移动时只能沿着水平或垂直方向移动的情况。
对于二维空间的曼哈顿距离代:
$ \text{distance} = |x_1 - y_1| + |x_2 - y_2| $
def manhattan_distance(point1, point2):
x1, y1 = point1
x2, y2 = point2
return abs(x1 - x2) + abs(y1 - y2)
欧几里得距离
适用于在连续空间中自由移动的情况,例如地图导航。
$ \text{distance} = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $
import math
def euclidean_distance(point1, point2):
x1, y1 = point1
x2, y2 = point2
return math.sqrt((x1 - x2)**2 + (y1 - y2)**2)
切比雪夫距离
适用于在网格状图中允许沿着对角线方向移动的情况。
$ h(n) = \max(|x_1 - x_2|, |y_1 - y_2|) $
def chebyshev_distance(node, goal):
x1, y1 = node
x2, y2 = goal
return max(abs(x1 - x2), abs(y1 - y2))
汉明距离
适用于计算两个相同长度字符串之间不同字符的数量,常用于字符串比较或拼图问题。
$ h(n) = \sum_{i=1}^{n} (s_i \neq t_i) $
# s1和s2长度相等,计算对应i下标不同的数目
def hamming_distance(s1, s2):
return sum(c1 != c2 for c1, c2 in zip(s1, s2))
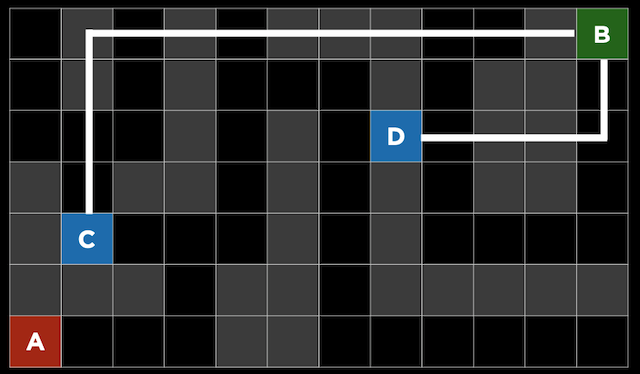
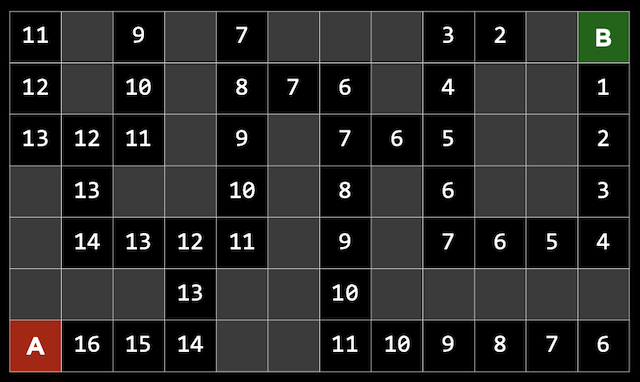
GBFS流程
有了评估的距离之后,GBFS过程如下,启发式函数使用曼哈顿距离:

A*
GBFS可能选择的不是最佳路径,如下图:
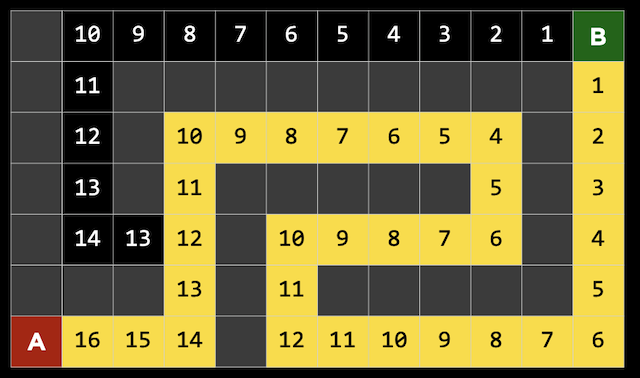
A*使用两个函数的和来判断路径选择, f(n) = g(n) + h(n)
g(n)=到达节点已经花费的代价
h(n)=预计到达终点的代价
A*流程

A*条件
若满足以下条件,则 A* 搜索是最优的:
- h(n)是可接受的(即从不高估真实代价),并且
- h(n)是一致的(对于每个节点n及其后继节点n’,具有步骤代价c,满足$ h(n) \leq h(n’) + c $)。
–End–