零和游戏
在零和游戏中(Zero-Sum Games),一方的收益等于另一方的损失。因此总收益和总损失的总和为零。这种游戏广泛应用于经济学、军事策略、决策理论和人工智能等领域。
与之相反的有正和游戏(Positive-Sum Game)和负和游戏(Negative-Sum Game)
MiniMax
极小极大算法(Minimax Algorithm)是一种穷举算法,因为它通过遍历所有可能的游戏状态来确定最佳策略。它通常用于决策制定和博弈论中的零和游戏,特别是在两人对抗性游戏中,如国际象棋、井字棋等。
井字棋
对于井字棋(Tic-Tac-Toe),X先手想获得最大值,O后手想获得最小值:
- 构建博弈树:从某一个状态开始,生成所有可能的下一步棋盘状态,直到游戏结束。
- 游戏终结点:例如,X赢得游戏的状态评估值为+1,X输掉游戏的状态评估值为-1,平局的状态评估值为0。
- 应用算法:这里是MiniMax, 可以看成BFS分层遍历,一层取最大值,一层取最小值,交替出现
PS: 由于AI采用的是最优策略,所以最好的情况是打成平局
实现代码
def minimax(board):
if terminal(board):
return None
optimal = None
value = None
is_x = player(board) == X
for action in actions(board):
if is_x:
tmp = min_value(result(board, action))
if value is None or tmp > value:
value = tmp
optimal = action
else:
tmp = max_value(result(board, action))
if value is None or tmp < value:
value = tmp
optimal = action
return optimal
def min_value(board):
if terminal(board):
return utility(board) # 如果是终点,返回评分
value = float('inf')
for action in actions(board):
value = min(value, max_value(result(board, action)))
return value
def max_value(board):
if terminal(board):
return utility(board) # 如果是终点,返回评分
value = float('-inf')
for action in actions(board):
value = max(value, min_value(result(board, action)))
return value
性能优化
棋盘有9个格子,每个格子有X,O或者EMPTY三种情况,所以最大的状态数$ 3^9 = 19{,}683 $
即使有效状态,对于9个格子的棋盘也会很大的数值
Alpha-Beta剪枝
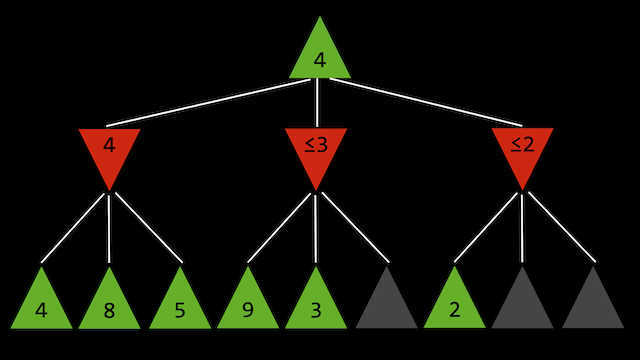
如图所示,由于绿色要取最大值max,红色要取最小值min, 对于灰色部分就没有计算的必要了
深度限制剪枝
设定一个最高访问深度,可以有效节省计算资源,缺点是结果可能不准确。
这里需要一个评估函数evaluation来返回某个状态下的期望评分,由于深度有限,游戏可能还没有结束。
评估函数的好坏,决定于AI的质量
def evaluation(state):
# [-1, 1]
return "期望utility数值"
def utility(state):
if "X赢得游戏":
return 1
elif "X输掉游戏":
return -1
else:
return 0
– END –