最小生成树
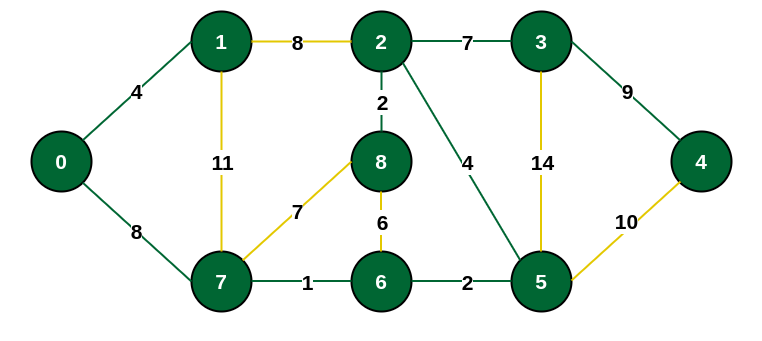
假设铺设道路,想通过最少的消耗,使得每个城市相互可达(上图绿色部分即为结果)
最小生成树特点如下:
- 无环性:最小生成树是一个连通的无环图。
- 连通性:最小生成树包括图中的所有顶点,并且所有顶点都是连通的。
- 边数:一个有 V 个顶点的图的最小生成树包含 V-1 条边。
Prim算法
该算法以任意点为起点,使用贪心策略,找到最小消耗向周围拓展一次。
然后,将联通的所有点看为一个整体,找到所有的可能拓展,使用小堆拿到最小值,在向周围拓展一次。
直到所有的边都被访问完成,检查是否全连通
from collections import defaultdict
import heapq
class Solution:
def minimum_cost(self, n: int, connections: List[List[int]]) -> int:
graph = defaultdict(list) # 使用字典记录图, dict[from] = (to, cost)
for x in connections:
graph[x[0]].append((x[1], x[2]))
graph[x[1]].append((x[0], x[2]))
heap = [(0, connections[0][0])] #任意点为初始点, [cost, city]
visited = set()
res = 0
while len(heap) > 0:
cost, city = heapq.heappop(heap)
if city in visited:
continue
visited.add(city)
res += cost
for node, node_cost in graph[city]:
if node not in visited:
heapq.heappush(heap, (node_cost, node))
return res if len(visited) == n else -1
Kruskal算法
该算法使用了数据结构并查集来处理连通性和个数
使用贪心策略,将边按照最小消耗排序,然后遍历排序后的所有边,直到所有的点连通上
class UnionFind:
def __init__(self, n):
self.nodes = [i for i in range(n + 1)]
self.count = [1 for i in range(n + 1)]
self.max_count = 1
def find(self, a):
if self.nodes[a] == a:
return a
self.nodes[a] = self.find(self.nodes[a])
return self.nodes[a]
def union(self, a, b):
root_a = self.find(a)
root_b = self.find(b)
if root_a != root_b:
self.nodes[root_a] = root_b
self.count[root_b] += self.count[root_a]
self.max_count = max(self.max_count, self.count[root_b])
print(self.max_count)
return True
else:
return False
class Solution:
def minimum_cost(self, n: int, connections: List[List[int]]) -> int:
connections.sort(key=lambda x: x[2]) # 按消耗从小到大排序
uf = UnionFind(n)
res = 0
for x in connections:
if uf.union(x[0], x[1]): # 如果没连接过,增加cost到结果
res += x[2]
return res if uf.max_count == n else -1
– END –