极客算法

OpenGL2.1 - 光模型Phong

2023-01-14
Graphics
 

颜色

每一种物体都有它自己的颜色，将无限的颜色映射到数字世界中，使用RGB模型，RGB是设备相关的颜色模型，每一种设备显示颜色会有不同。

glm::vec3 coral(1.0f, 0.5f, 0.31f);

物理世界中，我们看到的颜色，并不是物体的颜色，而是物体反色的光的颜色。

光的反射

物体的反色规则在显卡绘制中同样适用，定义光源的时候，指定一个颜色。

如果光源颜色与物体颜色相乘，结果将会反应出物体的视觉颜色(也就是物体反色光的颜色)

物体颜色的定义就是每一个颜色分量，物体能够反射的数值

例如白色光源与珊瑚红色物体:

glm::vec3 lightColor(1.0f, 1.0f, 1.0f);
glm::vec3 toyColor(1.0f, 0.5f, 0.31f);
glm::vec3 result = lightColor * toyColor; // = (1.0f, 0.5f, 0.31f);

绿色光源与同样物体, 可以看出物体吸收了一半的绿光，没有红色蓝色光可以反射,物体的视觉颜色也就变成了暗绿色

glm::vec3 lightColor(0.0f, 1.0f, 0.0f);
glm::vec3 toyColor(1.0f, 0.5f, 0.31f);
glm::vec3 result = lightColor * toyColor; // = (0.0f, 0.5f, 0.0f);

橄榄绿光源与同样物体

glm::vec3 lightColor(0.33f, 0.42f, 0.18f);
glm::vec3 toyColor(1.0f, 0.5f, 0.31f);
glm::vec3 result = lightColor * toyColor; // = (0.33f, 0.21f, 0.06f);

由此可以看出，相同的物体，会展示不同的视觉颜色

场景

光源

为了方便学习，需要画出光源位置，但是作为光源不希望被上面反射代码干扰，所以单独设置光源的Fragment Shader代码, Vertex Shader没有改动

Fragment Shader

#version 330 core
out vec4 FragColor;

void main()
{
    FragColor = vec4(1.0);
}

结果

源码

光影模型

物理世界的光影非常的复杂，OpenGL使用的简单的模型来模拟真实世界。

其中一种模型叫冯氏光照模型(Phong lighting), 主要结构由3个分量组成：环境(Ambient)、漫反射(Diffuse)和镜面(Specular)光照:

冯氏光照模型

  1. 环境(Ambient), 即使在夜晚，也会有一些光亮(比如月亮，星星)。所以，大部分场景物体不完全是漆黑的。Ambient常量用来模拟这种效果，用来给物体一些颜色。
  2. 漫反射(Diffuse)，用来模拟光源位置对物体的影响，是光模型中最重要的组成部分，物体的某一部分越是正对着光源，它就会越亮。
  3. 镜面(Specular), 模拟有光泽物体上面出现的亮点，它更接近光源的颜色。

环境光照

光源通常来自物体的各个方向，即使不是直接发光的物体。

光的一个特点是可以反射，通常光在一个空间里会反射的到处都是。

这些反射的光，会对物体产生间接的影响。global illumination会考虑这些反射。

我们这里采用global illumination里的一个非常简单的概念ambient lighting。

代码使用ambientStrength变量，这样环境就会始终有一些反射光存在

void main()
{
    float ambientStrength = 0.1;
    vec3 ambient = ambientStrength * lightColor;

    vec3 result = ambient * objectColor;
    FragColor = vec4(result, 1.0);
}

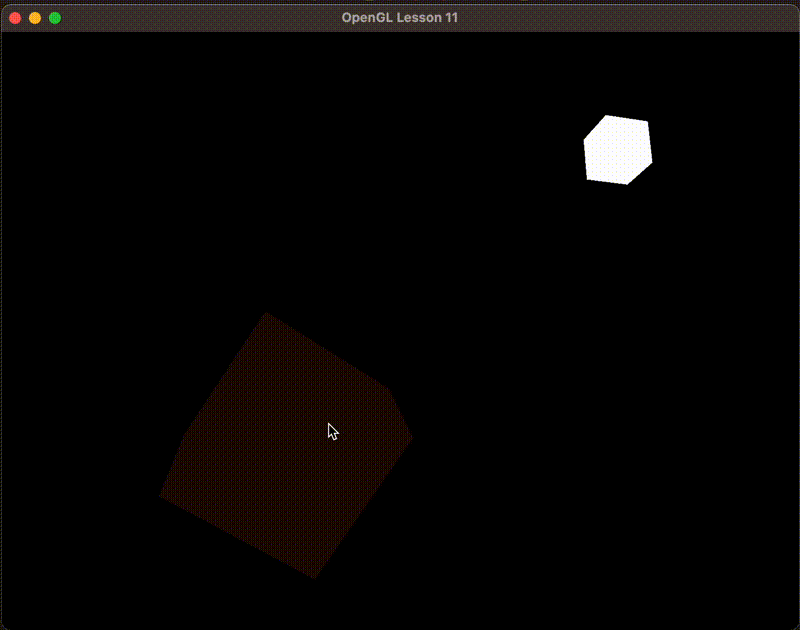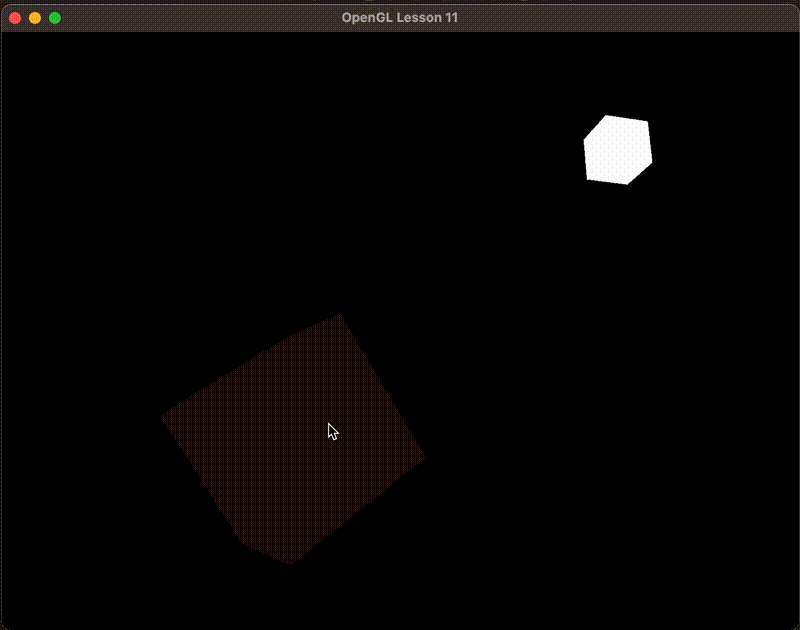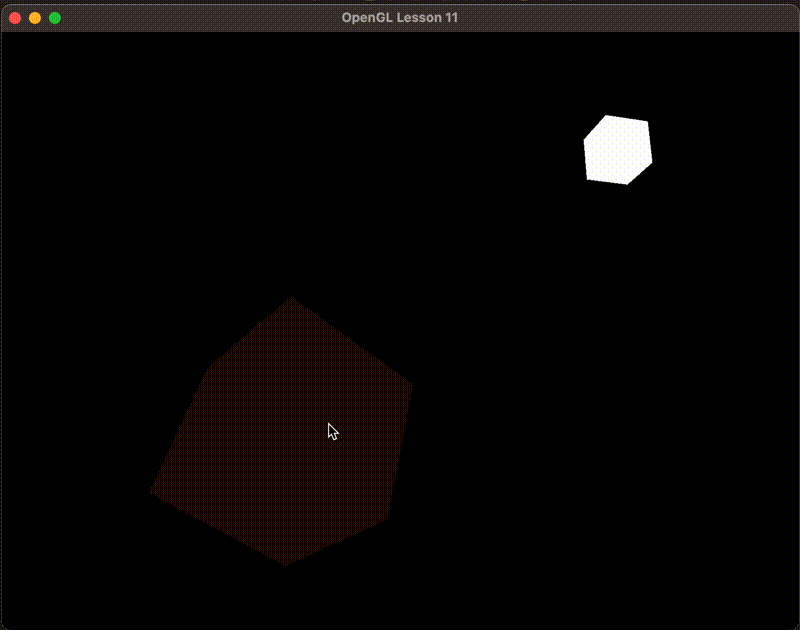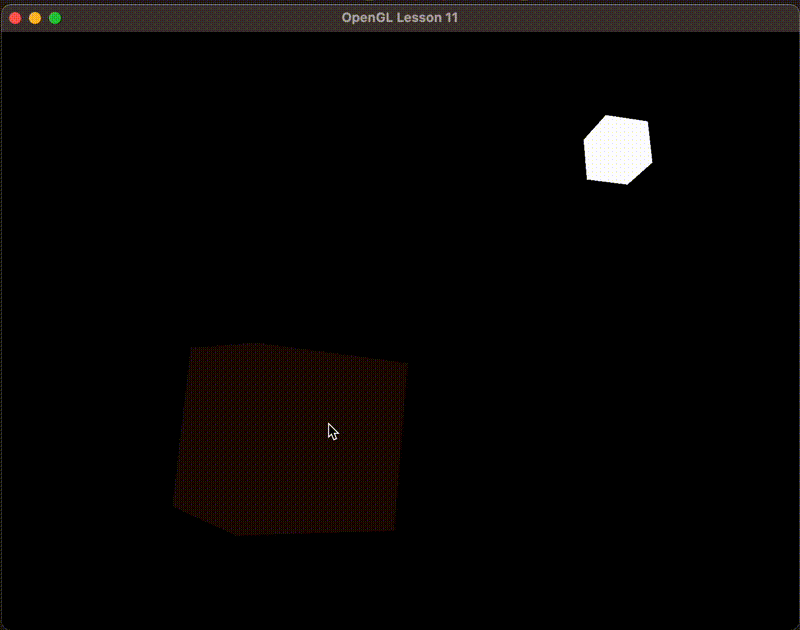
如下图，物体不是完全漆黑的，这就模拟了环境光照的效果

结果

漫反射光照

漫反射光会对物体颜色有明显的效果，离光源越近，就越亮。

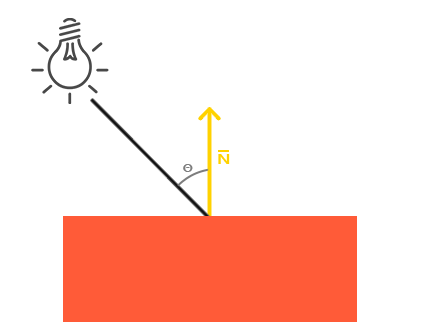
漫反射光照

图中，左边的光源发射光线到物体的一个Fragment上。 需要知道光线以什么角度射入的，如果光线是垂直照射的，光线就有最大的影响力(更亮)。

法向量

使用法向量(normal vector)来测量这个角度，也就是图中黄色的向量。角度可以用两个单位向量点乘获得。

$\theta$越小，单位向量点乘越接近1， 90度时为0。这与上面描述的漫反射影响效果一致

$ \vec{v}\cdot\vec{k} = ｜\vec{v}｜ * ｜\vec{k}｜ * \cos\theta $

向量点乘的结果，就反映了光源对物体各个Fragment影响程度。

法向量是垂直物体表面的单位向量, 因为单个vertex并不是平面，只是一个点。我们需要计物体体表面的法向量，可以通过周围的点组成的平面做向量叉乘获得。

漫反射计算

立方体法向量比较简单，直接放入vertex中, 然后再将数值传给Fragment Shader.

float vertices[] = {
    -0.5f, -0.5f, -0.5f,  0.0f,  0.0f, -1.0f,
     0.5f, -0.5f, -0.5f,  0.0f,  0.0f, -1.0f, 
     0.5f,  0.5f, -0.5f,  0.0f,  0.0f, -1.0f, 
     0.5f,  0.5f, -0.5f,  0.0f,  0.0f, -1.0f, 
    -0.5f,  0.5f, -0.5f,  0.0f,  0.0f, -1.0f, 
    -0.5f, -0.5f, -0.5f,  0.0f,  0.0f, -1.0f, 

    ... x5
]

定义光源的位置变量lightPos, 然后在程序中设施。

uniform vec3 lightPos;

最后，还需要Fragment的位置，光影是在世界空间完成的， 可以通过mode矩阵转换到世界空间，把结果传给Fragment Shader, 传参数时FragPos会被做差值处理

out vec3 FragPos;  
out vec3 Normal;

void main()
{
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    FragPos = vec3(model * vec4(aPos, 1.0));
    Normal = aNormal;
}

FragPos是世界的坐标，最后。 三个向量都有了，可以开始计算了

  1. 获取法向量
  2. 获得射入光线，通过向量差很容易获得，方向由被减数指向减数
  3. 通过点乘获取diff系数，然后乘以光源得到diffuse影响系数
  4. 合并ambient与diffuse在颜色个个分量上的影响系数
vec3 norm = normalize(Normal);
vec3 lightDir = normalize(lightPos - FragPos); 
float diff = max(dot(norm, lightDir), 0.0);
vec3 diffuse = diff * lightColor;

为了确保大于90的光线不会产生负值，将diff与0做max处理

注意，做光影计算的时候，通常只在乎向量的方向，所以会用normalize函数将向量转换成单位向量， 这样会简化计算。忘记normalize是一个常见的错误

结果

看上去怪怪的，主要是没有对法向量处理。使得光影停留在初始旋转时候的样子。

法线矩阵

法向量需要转换到世界空间， 但是直接乘会有问题。

首先，法向量只是一个方向向量，不能表达空间中的特定位置。同时，法向量没有齐次坐标（vertex位置中的w分量）。这意味着，位移不应该影响到法向量。因此，如果我们打算把法向量乘以model矩阵，我们就要从矩阵中移除位移部分，只选用模型矩阵左上角3×3的矩阵（注意，我们也可以把法向量的w分量设置为0，再乘以4×4矩阵；这同样可以移除位移）。对于法向量，我们只希望对它实施缩放和旋转变换。

其次，如果模型矩阵执行了不等比缩放，顶点的改变会导致法向量不再垂直于表面了。因此，我们不能用这样的model矩阵来变换法向量。下面的图展示了应用了不等比缩放的模型矩阵对法向量的影响：

结果

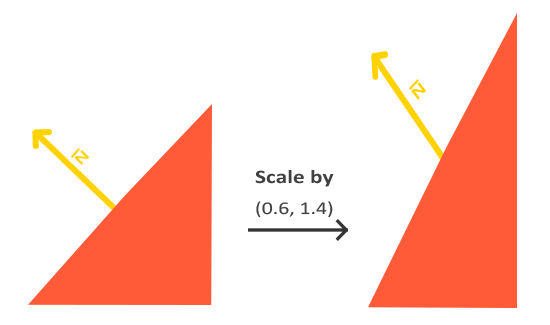
每当我们应用一个不等比缩放时（注意：等比缩放不会破坏法线，因为法线的方向没被改变，仅仅改变了法线的长度，而这很容易通过标准化来修复），法向量就不会再垂直于对应的表面了，这样光照就会被破坏。

修复这个行为的诀窍是使用一个为法向量专门定制的模型矩阵。这个矩阵称之为法线矩阵(Normal Matrix)

法线矩阵被定义为model矩阵左上角3x3部分的逆矩阵的转置.

Normal = mat3(transpose(inverse(model))) * aNormal;

注意，矩阵求逆是一项对于shaders开销很大，因为它必须在场景中的每一个Vertex上进行 最好先在CPU上计算出法线矩阵，再通过uniform把它传值 结果

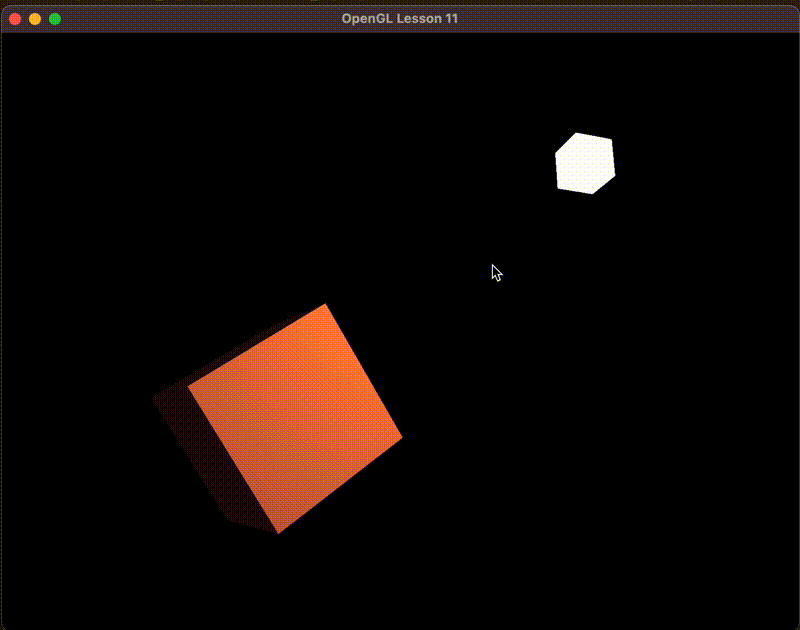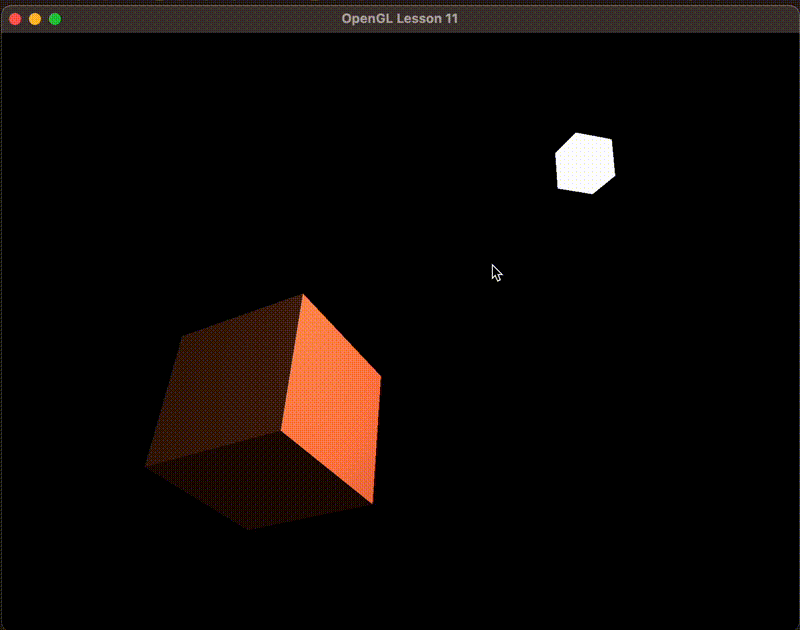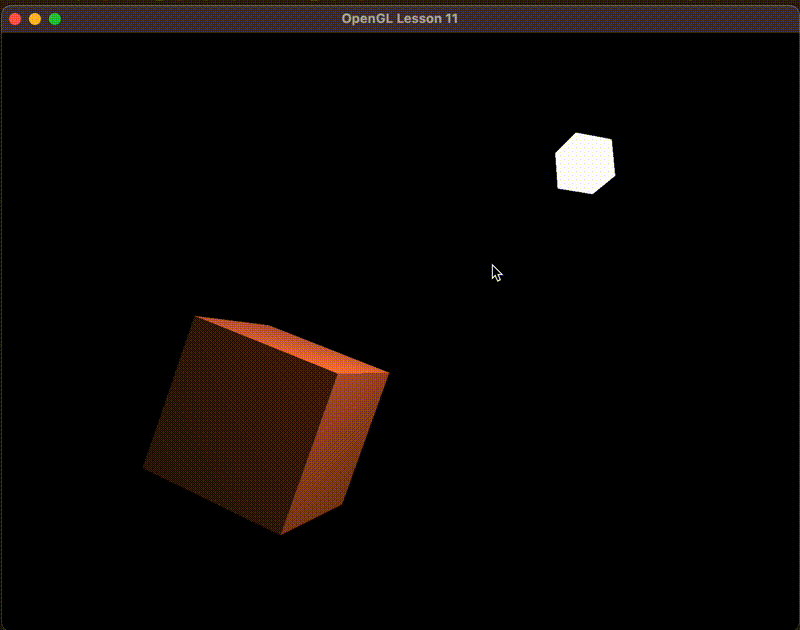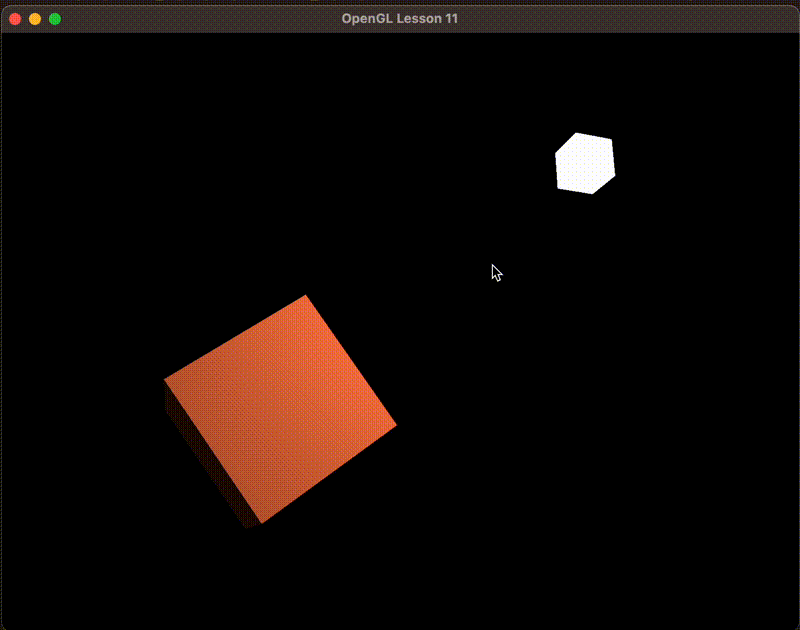
镜面光照

和漫反射光照一样，镜面光照也决定于光的方向向量和物体的法向量，但是它也决定于观察方向，例如玩家是从什么方向看向这个片段的。

物体表面的反射特性决定镜面光照。如果我们把物体表面设想为一面镜子，那么镜面光照最强的地方就是我们看到表面上反射光的地方。你可以在下图中看到效果：

镜面光照

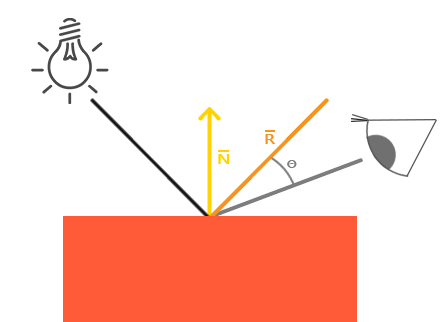
镜面光照计算

首先通过光的反射，得到反射光$\vec{R}$, 然后$\vec{R}$与观察方向的夹角$\theta$越小， 镜面光作用就越大。最后与其他分量叠加

观察点，即相机的位置，通过uniform来设定

uniform vec3 viewPos;
glUniform3f(glGetUniformLocation(shaderProgram, "viewPos"), cameraPos.x, cameraPos.y, cameraPos.z);

定义一个镜面强度specularStrength变量，给镜面高光一个中等亮度颜色，让它不要产生过度的影响。

float specularStrength = 0.5;

$\vec{viewPos} - \vec{FragPos}$获得从物体到眼睛的向量

vec3 viewDir = normalize(viewPos - FragPos);

reflect函数要求第一个向量是从光源指向片段位置的向量，但是lightDir当前正好相反，是从片段指向光源, 所以取负值

vec3 reflectDir = reflect(-lightDir, norm);

反光度

一个物体的反光度越高，反射光的能力越强，散射得越少，高光点就会越小。在下面的图片里不同反光度的效果

镜面光照

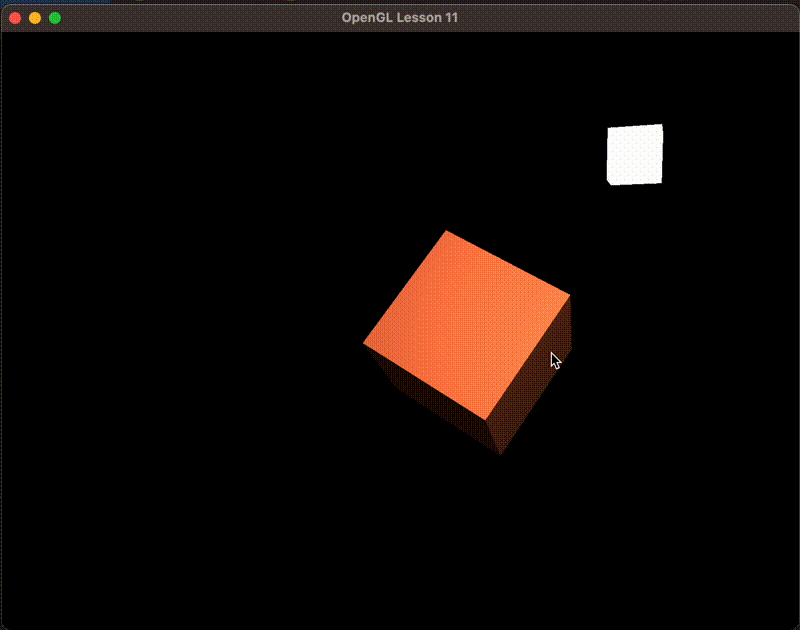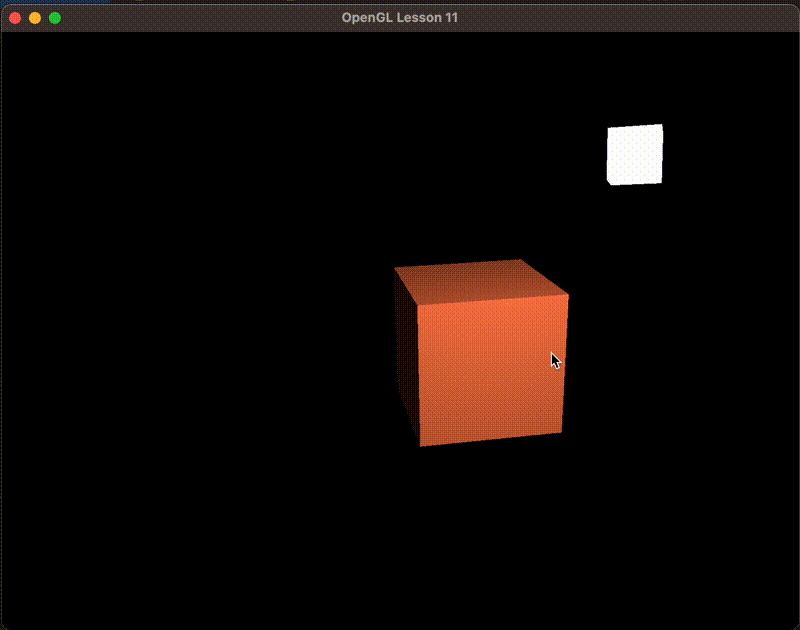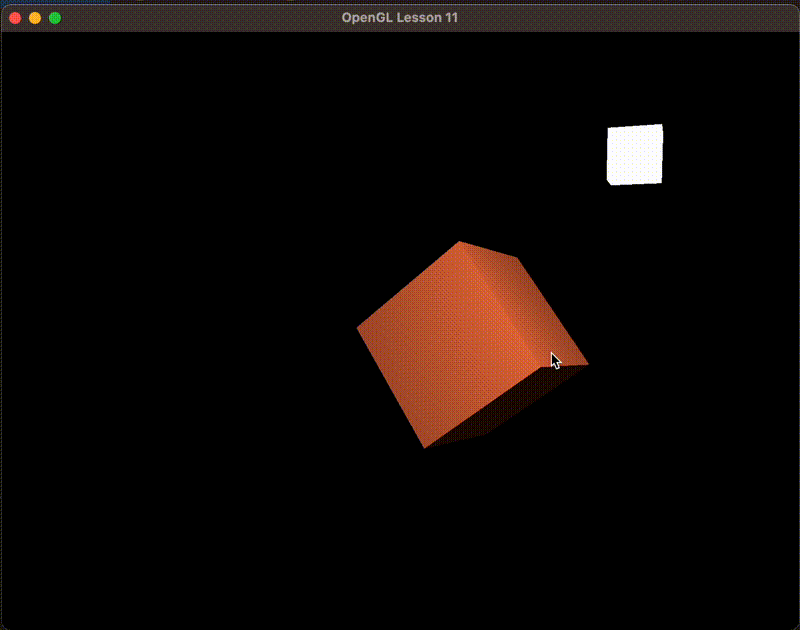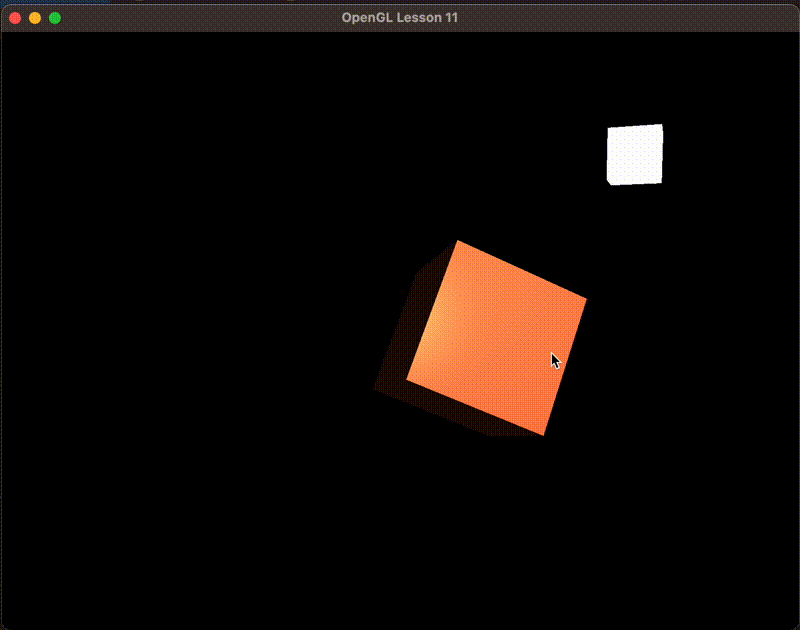
最后通过点乘计算影响系数，然后取32次方。这个32是反光度参数

float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);
vec3 specular = specularStrength * spec * lightColor;

结果

光照空间

这里选择在世界空间进行光照计算，但是大多数人趋向于更偏向在观察空间进行光照计算。

在观察空间计算的优势是，观察者的位置总是在(0, 0, 0)，所以你已经零成本地拿到了观察者的位置。

然而，若以学习为目的，在世界空间中计算光照更符合直觉。如果你仍然希望在观察空间计算光照的话，你需要将所有相关的向量也用观察矩阵进行变换（不要忘记也修改法线矩阵）。

光照对比

两种都采用冯氏光照模型，但处理位置不同：

在光照使用的的早期，开发者选择在vertex shader做光照处理，这种方法处理得快，只需要处理vertex数据就可以了，其余的值由插值完成。 这种在vertex shader处理的光照办法也叫Gouraud Shading

与之相反的是，在fragment shader做处理，好处是每个fragment都会有颜色处理，好处是颜色更加真实，也就是这节使用的方法Phong Shading

光照对比

源码

更多

  1. https://learnopengl.com/Lighting/Basic-Lighting
  2. http://www.lighthouse3d.com/tutorials/glsl-12-tutorial/the-normal-matrix/

相关推荐

上一篇 OpenGL1.8 - 相机Camera

下一篇 技术分析 - K线图

评论

内容:
其他: